http://phpwebquest.org/newphp/miniquest/soporte_tabbed_m.php?id_actividad=43962&id_pagina=1
Muy importante para empezar:http://www.cidse.itcr.ac.cr/cursos-linea/SUPERIOR/t2-Funciones-de-variasvariables/4-curvas-superficies/index.html
Graficar Online: http://www.solvemymath.com/online_math_calculator/plots_geometry/3d_graphing_calculator/index.php
¿¿Gráficas de superficies 3D con Excel?? (wtf): http://www.cidse.itcr.ac.cr/revistamate/HERRAmInternet/TecnologiasIntv3n3/node6.htm
Este espacio fue creado para cargar contenidos referentes al cálculo diferencial
jueves, 28 de julio de 2011
Clases en el Profesorado
Aquí subo una síntesis de las clases de cálculo superior que tengo a mi cargo:
Cilindros Parabólicos
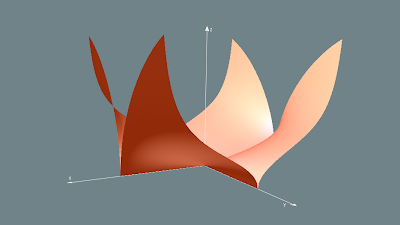
A continuación se observarán las gráficas de de las superficies:
z= x2
z= x2
z= y2
El objetivo aquí es ver de qué manera cambia la superficie en cuanto se cambia la variable afectada por el exponente 2.
 |
z= y2 |
Introducción a las Superficies Cilíndricas
Para comenzar, lo haremos con un tipo simple de superficies, "Los Cilindros", y seguro que al escuchar la palabra cilindro, esta nos recuerda:

Pero para poder determinarla de la manera que nosotros queremos, se deberá considerar la siguiente expresión en tres dimensiones:

Pero para poder determinarla de la manera que nosotros queremos, se deberá considerar la siguiente expresión en tres dimensiones:
x2 + y2 = 9
Lo primero que uno podría pensar que dicha expresión pertenece a una circunferencia de radio 3, pero eso solo es correcto en parte, si nos limitáramos solo a los dos dimensiones.
¿ Pero en las tres dimensiones que ocurrirá?
Analicemos la intersección con cada plano z = k. (se deberá imaginar planos paralelos al plano formado por los ejes x e y).
¿Qué significa esto?
Que k será una constante (puede ser cualquier valor numérico), y seguidamente se observará lo que sucede con la expresión x2 + y2 = 9 cada vez que le damos a Z un valor distinto.
Pero en esta ocasión se puede observar que la variable Z está ausente de la ecuación, tal intersección (que se llama traza de la superficie en el plano = k) es siempre la misma: una circunferencia de radio 3.
¿Qué superficie corta a todo plano paralelo al plano xy en una circunferencia de radio 3?
Claro está que es un cilindro circular recto, en este caso de radio 3 y con eje en el eje z.
En general, el término cilindro se usa para referirse a cualquier superficie cuyas trazas en todo plano paralelo a otro plano dado son idénticas. Con esta definición, muchas superficies resultan ser cilindros.
Softwares utilizados
Los programas informáticos que serán de mucha ayuda (entre otros) son: Mathematica 7 y el Zhu3d
Bajar Mathemática de aquí: http://www.megaupload.com/?d=NHFNCLF6
Bajar Zhu3d de aquí: http://zhu3d.uptodown.com/
Bajar Mathemática de aquí: http://www.megaupload.com/?d=NHFNCLF6
Bajar Zhu3d de aquí: http://zhu3d.uptodown.com/
Superficies en el Espacio
No esperes aquí a una teoria general como en las dos dimensiones. Dibujar a mano curvas y superficies en el espacio, o interpretar gráficas generadas por calculadoras o computadoras, es casi un arte.
Pero tampoco mi objetivo es formar un artista, sino aportar ideas y herramientas para representar ciertas clases de superficies que pueden resultar necesarias para estudios superiores del cálculo.
Pero tampoco mi objetivo es formar un artista, sino aportar ideas y herramientas para representar ciertas clases de superficies que pueden resultar necesarias para estudios superiores del cálculo.
Suscribirse a:
Comentarios (Atom)